書籍分享天地

書-深度學習的數學

​​

●數列

○數列的通項公式

●數列與遞推關系式

○聯立遞推關系式

數列

數的序列，以下被稱為偶數的數列。

2，4，6，8...

第一項稱首項，第二位稱為第2項，第n位被稱為第n項，如果是有窮數列，最後一項稱為末項。

下面這個稱有窮數列(可以看到底)。

1，3，5，7，9，11

首項1，末項11，項數6

數列的通項公式

第n個數列會用an表示，a為此數列的名字(以拉丁、希臘字母表示)，要表示整個數列就用集合符號{a}來表示。

第n項可以用式子表示就稱'通項公式'。

例:

試求{b} = {1, 3, 5, 7, 9}的通項公式。

bn = 2n-1。

我們來看神經元層數的表達:

第l層的第j個神經元。

數列與遞推關系式

通項公式用來表示項的式子，還有另一種表示法'遞推關系式'，以相鄰兩項an、an+1的關係式。

例:

已知首項a1 = 1，關系式，用遞推關系式算出數列。

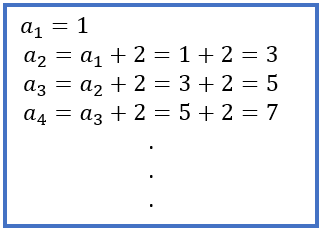
例:

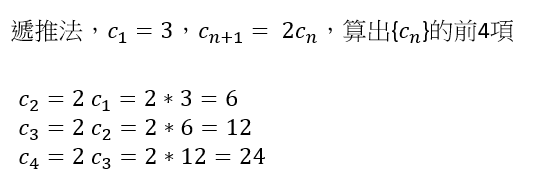
例:

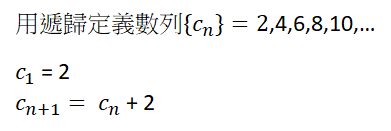
聯立遞推關系式

多個遞推關系式所組成，稱聯立遞推關系式。

神經網路的輸入輸出都可以用聯立的方式表達，看下下圖可以寫出下面的聯立。

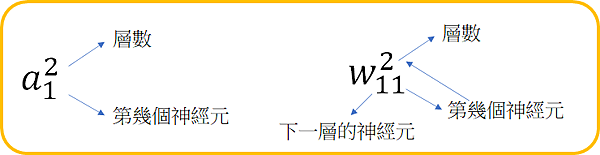
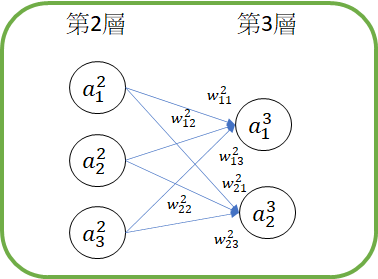
a:神經元

w:權重

b:偏置

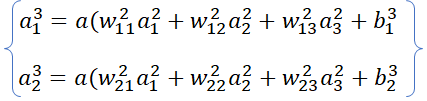
後面會講到誤差反向傳播，就是用遞推的方式。