書-深度學習的數學

神經網路所需的函數-一次函數
自變量
神經網路所需的函數-二次函數
單位階躍函數
指數函數與Sigmoid函數
正態分布的概率密度函數
神經網路所需的函數-一次函數
1.一次函數
介紹: 最基本的函數。
公式: y = ax + b (a、b為常數, a0)
a = 斜率 , b = 截距
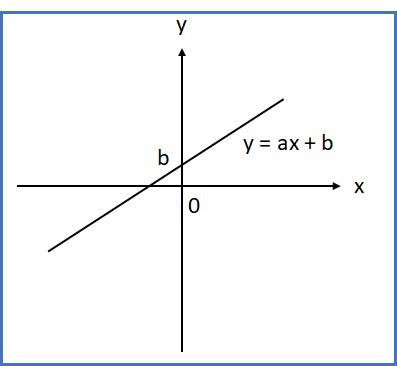
例:
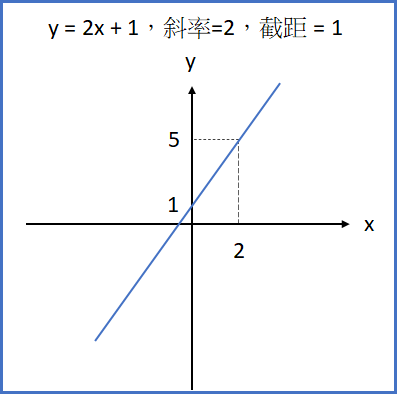
一次函數也可以用於多個變數。
y = ax1 + bx2 + c (a、b、c為常數,a0, b0)
例:
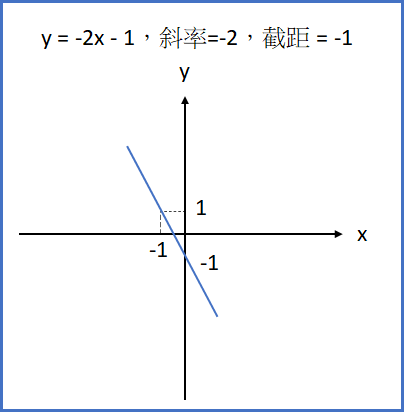
自變量
如果x確定只與y有對應,則稱y是x的函數,y = f(x),x稱為'自變數',y稱為'因變數'
神經網路所需的函數-二次函數
介紹: 與一次函數一樣重要,這本書的代價函數就是使用二次函數。
公式: y = ax2 + bx + c (a、b、c為常數,a0)
二次函數的圖就像拋物線的軌跡,a為正數是向下凸,而取得最小值,這個性質要講到最小二乘法的基礎。
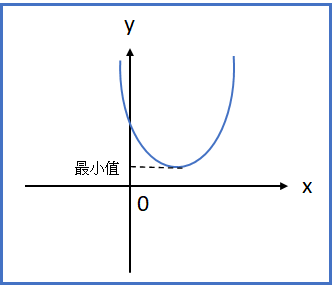
例:
當x = 1時,取得最小函數2。
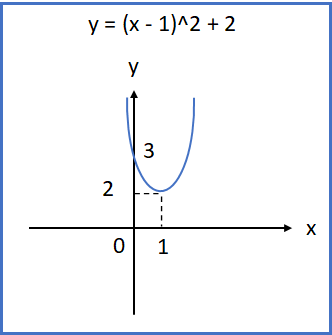
例:
多個自變量。
公式: y = ax2 + bx1x2 + cx22 + px1 + qx2 + r (a、b、c、p、q、r為常數、c0)
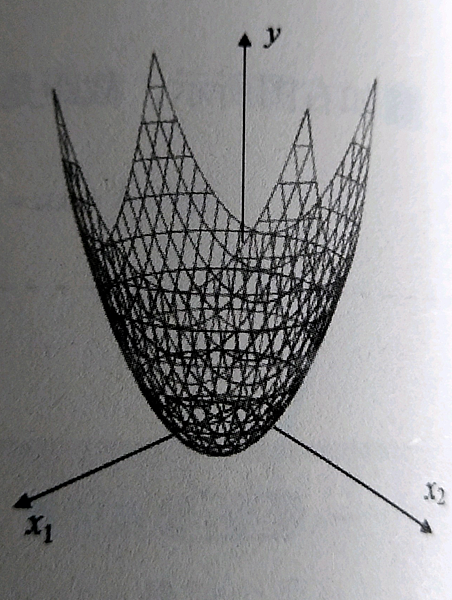
例:
單位階躍函數
介紹:作為激活函數(就是輸出經過的最後一個函數)。
在原點不連續,也就是原點不可導,就是這個性質所以不能成為主要的激活函數。
式子:
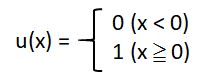
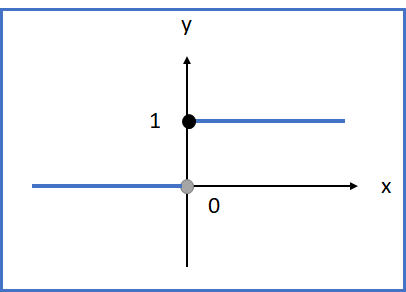
例:
u(-1) = 0
u(1) = 1
u(0) = 0
指數函數與Sigmoid函數
介紹: 具有以下形狀的函數稱為'指數函數'
常數a成為指數的底數,納皮爾數e是個重要的底數,e = 2.71828...。
公式: y = ax (a為正整數,a1)
Sigmoid函數σ(x)
介紹: 是最具有代表性的激活函數。
公式:
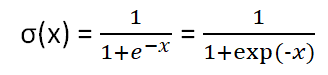
exp是exponential function(指數函數)的簡略記法,exp(x)表示指數函數ex。
值介於01之間式連續的因此是可以導的,也可以用來解釋機率。
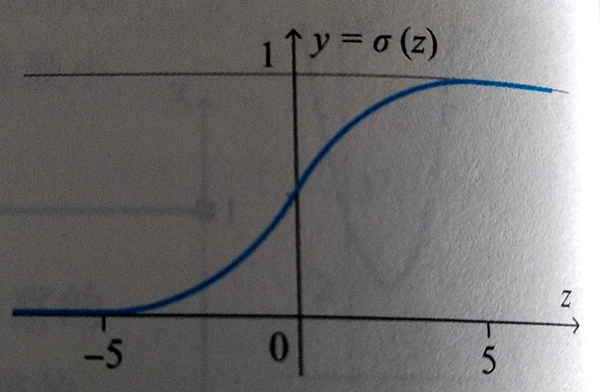
例:
σ(-1) = 0.27
σ(0) = 0.5
σ(1) 0.73


正態分布的概率密度函數
設置權重與偏置的初始值,正態分布(normal distribution )是一個有用的工具。
分布機率:
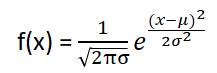
其中μ稱為期望值(平均值),σ稱為標準差。
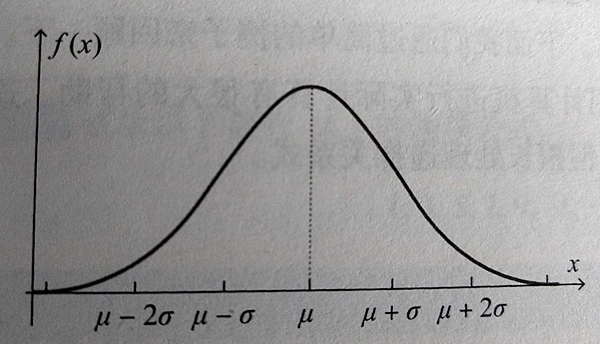
例:
期望值(μ)為0,標準差(σ)為1的機率密度函數。
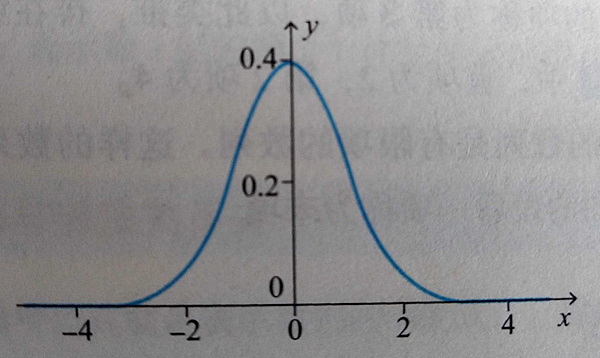
正態分布產生得隨機樹稱為正態分布隨機數,在神經網路計算中,用於初始值。

