書-深度學習的數學
●柯西-施瓦茨不等式
○內積的座標表示
●向量的一般化
柯西-施瓦茨不等式
內積公式: a‧b=|a||b|cosθ
根據我們的內積公式可以得出柯西-施瓦茨(ㄘˊ)不等式。
柯西-施瓦茨(ㄘˊ)不等式: -|a||b|≤a‧b≤|a||b|
證明:
根據余弦函數的性質(余弦函數的極小值跟極大值是[-1,1])，對任意θ，有乘|a||b|，有
-|a||b|≤|a||b|cosθ≤|a||b|
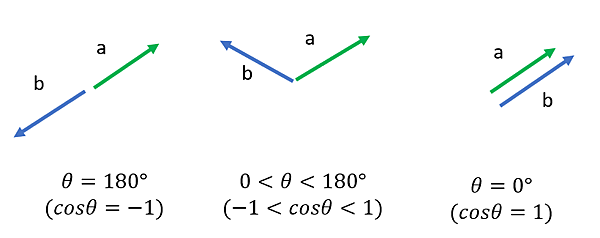
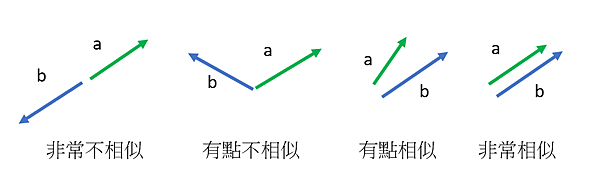
根據內積來知道兩個向量的相似度。
內積的座標表示
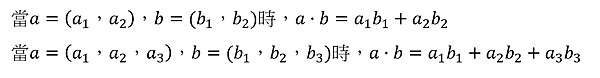
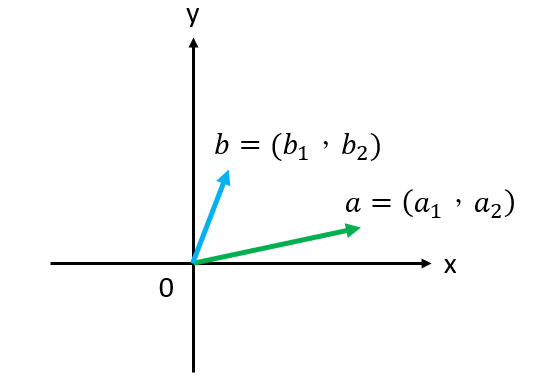
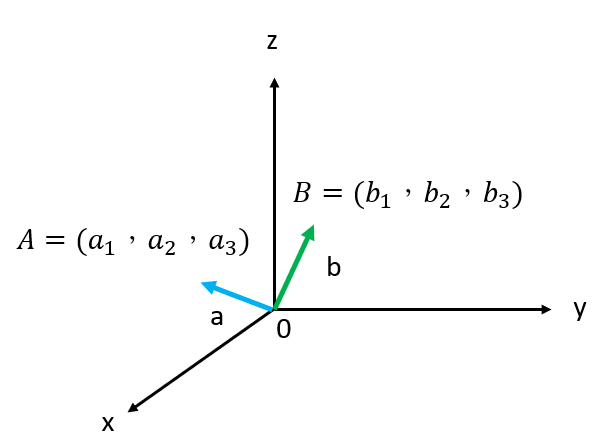
有些文獻會用上面兩個當作內積的定義。
二維:
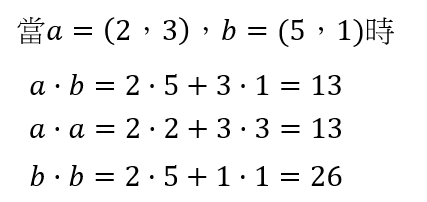
三維:
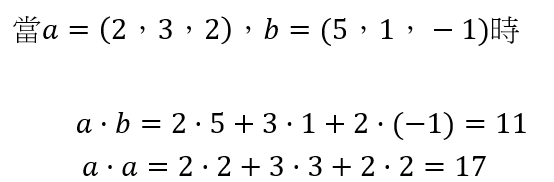
求a、b向量的內積
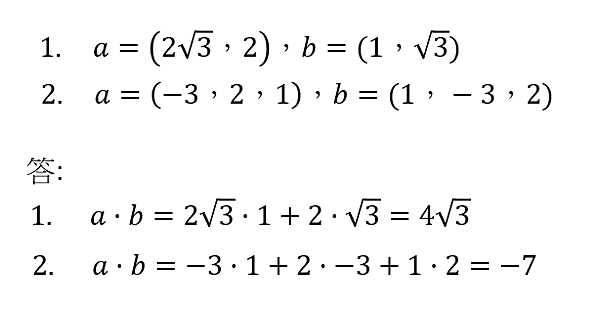
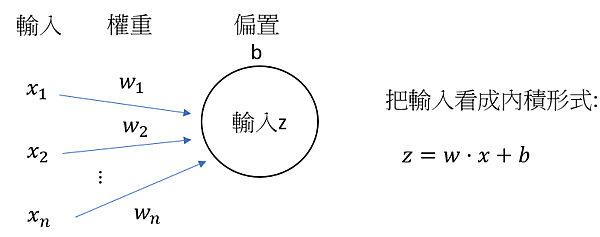
向量的一般化
看了二維&三維空間的性質，雖說神經網路要處理數萬維的空間，但是二維跟三維空間的性質可以直接使用，向量被運用在梯度下降法中，我們先看如何把二維&三維空間中的向量公式用到n維空間中。
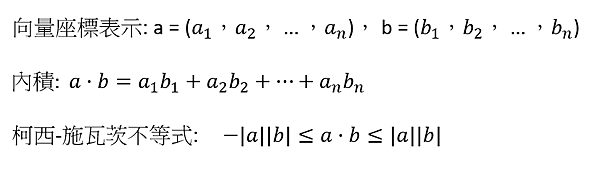
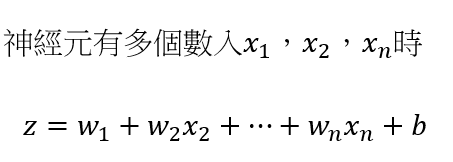
文章標籤
全站熱搜
留言列表